UNIDAD 1: LA INTELIGENCIA ARTIFICIAL EN LA INGENIERÍA

1.1   DEFINICION La Inteligencia Artificial es una rama de la informática que estudia la inteligencia e intenta imitarla de forma artificial. Pero la inteligencia es un término que todavía no se ha conseguido definir de manera unánime por todas las ciencias. Por ejemplo, muchas personas se refieren a la inteligencia de los animales. ¿Es un animal inteligente? ¿Es el mbre más inteligente que el animal? El primero que estudió estos temas fue Alan Turing que se planteó si se podría construir algún día una máquina que fuera tan inteligente como un ser humano. Se planteó cuál sería el momento en el que podríamos decir que una máquina es tan inteligente como un ser humano. De este modo enunció su famosa "Prueba de Turing", ésta consiste en colocar nuestra máquina inteligente y a un ser humano frente a frente, pero sin poder verse. Se iniciaría una conversación sobre algún tema. Según Turing, una máquina sería inteligente si el ser humano no distinguiera si es una máquina u otra persona con la que está hablando.   1.2   AREAS DE APLICACION Pero también hay áreas de aplicación. En efecto, estos procesos de la AI se Aplican en los sistemas reales en una gran variedad de ramas y problemas: • Gestión y control: análisis inteligente, fijación de objetivos. • Fabricación: diseño, planificación, programación, monitorización, control, gestión de proyectos, robótica simplificada y visión computarizada. •Educación: adiestramiento práctico, exámenes y diagnóstico. •Ingeniería: diseño, control y análisis. •Equipamiento: diseño, diagnóstico, adiestramiento, mantenimiento, configuración, monitorización y ventas. • Cartografía: interpretación de fotograf ías, diseño, resolución de problemas cartográficos. • Profesiones: abogacía, medicina, contabilidad, geología, química. • Software: enseñanza, especificación, diseño, verificación, mantenimiento. • Sistemas de armamento: guerra electrónica, identificación de objetivos, control adaptativo, proceso de imágenes, proceso de señales. • Proceso de datos: educación, interfase en lenguaje natural, acceso inteligente a datos y gestores de bases de datos, análisis inteligente de datos. • Finanzas: planificación, análisis, consultoría.             1.3   METODOS INTELIGENTES  1.         La lógica difusa: permite tomar decisiones bajo condiciones de incerteza. 2.         Redes neuronales: esta tecnología es poderosa en ciertas tareas como la clasificación y el reconocimiento de patrones. Está basada en el concepto de "aprender" por agregación de un gran número de muy simples elementos. Este modelo considera que una neurona puede ser representada por una unidad binaria: a cada instante su estado puede ser activo o inactivo. La interacción entre las neuronas se lleva a cabo a través de sinapsis. Según el signo, la sinapsis es excitadora o inhibidora. El perceptrón está constituido por las entradas provenientes de fuentes externas, las conexiones y la salida. En realidad un perceptrón es una Red Neuronal lo más simple posible, es aquella donde no existen capas ocultas. Para cada configuración de los estados de las neuronas de entrada (estímulo) la respuesta del perceptrón obedece a la siguiente dinámica: se suman los potenciales sinápticos y se comparan con un umbral de activación. Esta suma ponderada es también llamada campo. Si el campo es mayor que un umbral, la respuesta de la neurona es activa, si no, es inactiva. Con una arquitectura tan simple como la del perceptrón no se puede realizar más que una clase de funciones "booleanas" muy simples, llamadas linealmente separables. Son las funciones en las cuales los estados de entrada con salida positiva pueden ser separados de aquellos a salida negativa por un hiperplano. Un hiperplano es el conjunto de puntos en el espacio de estados de entrada, que satisfacen una ecuación lineal. En dos dimensiones, es una recta, en tres dimensiones un plano, etc. Si se quieren realizar funciones más complejas con Redes Neuronales, es necesario intercalar neuronas entre las capas de entradas y de salida, llamadas neuronas ocultas. Una red multicapas puede ser definida como un conjunto de perceptrones, ligados entre si por sinapsis y dispuestos en capas siguiendo diversas arquitecturas. Una de las arquitecturas más comúnmente usada es llamada feedforward: con conexiones de la entrada a las capas ocultas y de éstas hacia la salida. El funcionamiento de una Red Neuronal es gobernado por reglas de propagación de actividades y de actualización de los estados. 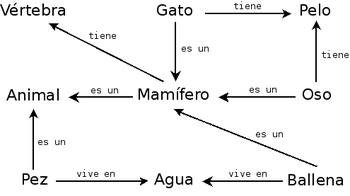1.4   REDES SEMANTICAS Una red semántica o esquema de representación en Red es una forma de representación de conocimiento lingüístico en la que los conceptos y sus interrelaciones se representan mediante un grafo. En caso de que no existan ciclos, estas redes pueden ser visualizadas como árboles. Las redes semánticas son usadas, entre otras cosas, para representar mapas conceptuales y mentales. Un ejemplo de red semántica. En un grafo o red semántica los elementos semánticos se representan por nodos. Dos elementos semánticos entre los que se admite se da la relación semántica que representa la red, estarán unidos mediante una línea, flecha o enlace o arista. Cierto tipo de relaciones no simétricas requieren grafos dirigidos que usan flechas en lugar de líneas. 1.5  INTELIGENCIA DISTRIBUIDA Autores como Salomon (1993) o Resnick y Collins (1996) afirman que la cognición al igual que las herramientas, artefactos y sistemas simbólicos son saberes compartidos por los individuos de manera tal que el pensamiento estaría situado y distribuido socialmente en contextos particulares de intenciones, compañeros e instrumentos. David Perkins junto con Roy Pea hablan de Inteligencia Distribuida y Cognición Distribuida respectivamente. La Inteligencia Distribuida está constituida por los recursos cognitivos del ser humano además de todas las herramientas que ha desarrollado a lo largo de la civilización. Deberíamos, entonces, aprender a utilizar inteligente y pertinentemente los recursos del entorno para potenciar nuestros aprendizajes. Roy Pea prefiere referirse al término Cognición Distribuida (en la obra con ese título) como aquellos saberes que están presentes en diferentes personas y que, al compartirse, pasan a ser apropiados por los compañeros del grupo. Indudablemente, las teorías revisadas reflejan las numerosas facetas y la multilateralidad de la inteligencia y creo indispensable un esfuerzo de coordinación entre ellas para lograr un entendimiento holista de lo qué es la inteligencia y de cómo se compone. Así pues, la inteligencia no sólo está relacionada con la capacidad cognitiva del ser humano sino que abarca otro tipo de habilidades que irían desde las mentales hasta las emocionales logrando dar una visión de las personas no sólo en cuanto a su pensar inteligente sino también a su hacer, sentir y convivir. La actividad inteligente implica una multiplicidad de capacidades, estructuras y procesos de carácter contextual, personal, social, cultural que abarcan desde capacidades mentales para adquirir nuevo conocimiento, resolver problemas, ajustarse a nuevas situaciones, usar conceptos o combinar información novedosamente hasta capacidades personales y socioculturales para percibir y entender las emociones propias y ajenas, compartir y distribuir saberes y recursos y tener éxito personal y social en el diario vivir.

UNIDAD 2: CALCULO DE PREDICADOS

2.1 ELEMENTOS BASICOS Un lenguaje como el cálculo de predicados está definido por una sintaxis un alfabeto de símbolos, que ordenados adecuadamente da origen a expresiones válidas llamadas formulas bien formadas (wff). Los componentes del cálculo de predicados son símbolos de: predicados, constantes, paréntesis,corchetes, comas, las constantes lógicas Verdadero y Falso, los 5 conectores lógicos: negación (Ø), y lógica (Ù), o lógica (Ú), implicación (Þ), y doble implicación (Û) Estos componentes siguiendo reglas de la gramática como por ejemplo, la de Backus-Naur, BNF (Backus-Naur Form), constituyen oraciones (Proposiciones) o wff. Los componentes del cálculo de predicados son símbolos de: predicados, variables, constantes, paréntesis, corchetes y comas y las constantes Lógicas Verdadero, Falso. Predicados: Representan hechos en el dominio del discurso. Si se les da un significado (Semántica) los predicados devuelven un valor de verdad (verdadero o falso), se representan por letras mayúsculas, Constantes: (sustantivos), representan objetos del dominio, se simbolizan por letras mayúsculas se diferencian de los predicados por el contexto. Los paréntesis, comas y corchetes son separadores, para mejorar la legibilidad (y el cómputo) Las fórmulas mínimas se llaman formulas atómicas, representan hechos en el dominio del discurso, y representan el conocimiento que se tiene del mundo, o la base de conocimientos (BC).

2.2 REPRESENTACION La principal debilidad de la lógica proposicional es su limitada habilidad para expresar conocimiento. Existen varias sentencias complejas que pierden mucho de su significado cuando se las representa en lógica proposicional. Por esto se desarrolló una forma lógica más general, capaz de representar todos los detalles expresados en las sentencias, esta es la lógica de predicados. La lógica de predicados está basada en la idea de las sentencias realmente expresan relaciones entre objetos, así como también cualidades y atributos de tales objetos. Los objetos pueden ser personas, objetos físicos, o conceptos. Tales cualidades, relaciones o atributos, se denominan predicados. Los objetos se conocen como argumentos o términos del predicado. Al igual que las proposiciones, los predicados tienen un valor de veracidad, pero a diferencia de las preposiciones, su valor de veracidad, depende de sus términos. Es decir, un predicado puede ser verdadero para un conjunto de términos, pero falso para otro. Por ejemplo, el siguiente predicado es verdadero: color (yerba, verde) el mismo predicado, pero con diferentes argumentos, puede no ser verdadero: color (yerba, azul) o color (cielo, verde) Los predicados también pueden ser utilizados para asignar una cualidad abstracta a sus términos, o para representar acciones o relaciones de acción entre dos objetos. Por ejemplo: mortal(juan_carlos)      clima(martes, lluvioso) ave(gaviota) ama(roberto, vanessa) lee(alex, novela) mordio(boby, cartero) Al construir los predicados se asume que su veracidad está basada en su relación con el mundo real. Naturalmente, siendo prácticos, trataremos que los predicados que definimos estén de acuerdo con el mundo que conocemos, pero no es absolutamente necesario que así lo hagamos. En lógica de predicados el establecer como verdadero un predicado es suficiente para que así sea considerado. Demos el siguiente ejemplo, que indica que Ecuador está en Europa: parte_de(ecuador, europa) Obviamente, esto no es verdadero en el mundo real, pero la lógica de predicados no tiene razón de saber geografía y si el predicado es dado como verdadero, entonces es considerado como lógicamente verdadero. Tales predicados, establecidos y asumidos como lógicamente verdaderos se denominan axiomas, y no requieren de justificación para establecer su verdad.

2.3 UNIFICACION Por ejemplo en Lógica Proposicional la contradicción es evidente porque  Pero en Cálculo de Predicados es diferente porque si tengo: Estudia(x) ^ ¬Estudia(y) . no hay contradicción     P(a) y P(x) no son comparables, para que lo sean, se debe encontrar una substitución para x que haga ambas fórmulas idénticas. Este proceso de encontrar una sustitución para hacer fórmulas idénticas  se conoce como unificación.    Lo que se puede sustituir en una fbf para permitir el pareamiento de dos fórmulas son las variables por términos. Variable (Símbolos de constantes, Símbolos de variables, expresiones funcionales)

2.4 RESOLUCION Es una regla de inferencia usada en la deducción computacional, debido a que es eficiente ya que trabaja sobre sentencias que han sido transformadas a una forma canónica llamadas cláusulas disyuntivas. Este proceso de resolución obtiene demostraciones por refutación. Es decir, para probar una proposición (su validez) se intenta demostrar que su negación lleva a una contradicción con las proposiciones conocidas (es decir es insatisfactible).     No hay una atribución de verdad que satisfaga el ejemplo anterior.

UNIDAD 3: SISTEMAS DE PRODUCCIÓN

3.1  Representación de problemas como  sistema de producción La incorporación de agentes de decisión inteligente, redes neuronales, sistemas expertos, algoritmos genéticos y autómatas programables para optimización de sistemas de producción es una tendencia activa en el ambiente industrial de países con alto desarrollo tecnológico y con una gran inversión en investigación y desarrollo. Dichos componentes de la Inteligencia Artificial tienen como función principal controlar de manera independiente, y en coordinación con otros agentes, componentes industriales tales como celdas de manufactura o ensamblaje, y operaciones de mantenimiento    3.2   Mecanismos de inferencia El mecanismo de inferencia es la unidad lógica con la que se extraen conclusiones de la base de conocimientos, según un método fijo de solución de problemas que esta configurado imitando el procedimiento humano de los expertos para solucionar problemas.     Una conclusión se produce mediante aplicación de las reglas sobre los hechos presentes. Ejemplo. Una Regla es: Si p y q entonces r p y q son justo aquellos hechos que se mencionan en la cláusula "si" de la regla, es decir, las condiciones para la aplicabilidad de la regla. Aplicar la regla es: deducir de los hechos p y q el hecho r.    3.3  Resolución de conflictos La resolución de conflictos se aplica sobre un conjunto de reglas que pueden ser desencadenables (reglas que cazan con las condiciones pero todavía no han pasado a la memoria de trabajo (MT). Con esto se evita su almacenamiento en la MT. 1. Orden de las reglas en la base de conocimientos. 2. Reglas con mayor coeficiente de credibilidad 3. Reglas con menor número de cláusulas a instanciar. 4. Reglas con mayor número de conclusiones. 5. Reglas menos complejas. 6. Descartar las reglas ya utilizadas. 7. Reglas con mayor numero de condiciones La heurística muchas veces puede provocar que el problema no tenga solución (producto de las podas del árbol), sin embargo las sistemáticas siempre hayan la solución    3.4  Mecanismo de explicación  Los mecanismos de explicación, la parte más fascinante de los sistemas expertos, permiten a los sistemas explicar o justificar sus conclusiones, y también posibilitan a los programadores verificar el funcionamiento de los propios sistemas. Los sistemas expertos comenzaron a aparecer en la década de 1960. Sus campos de aplicación son la química, la geología, la medicina, la banca e inversiones y los seguros.      3.5  Busquedas Las técnicas de solución de problemas en IA, en general, incorporan un proceso de búsqueda. Todo proceso de búsqueda puede ser visualizado como el recorrido por un árbol en el que cada nodo representa un estado y cada rama representa las relaciones entre los estados cuyos nodos conecta. A continuación se describen los algoritmos de tres procesos básicos de búsqueda de soluciones en el espacio de estado. Algoritmo Generación Y Prueba (GENERATE-AND-TEST) 1. Generar una posible solución. (estado o camino) 2. Comprobar para ver si es una solución, mediante comparación con los elementos del conjunto de objetivos aceptables. 3. Si la solución ha sido encontrada salir, de otra manera, retornar al paso 1. Algoritmo Primero a lo Ancho (BREATH-FIRST) 1.Crear una variable NODE_LIST y ponerla al estado inicial. a.Remover el primer elemento de NODE_LIST, y llamarlo E. Si NODE_LIST estuvo vacía, salir. i.Aplicar la regla para generar un nuevo estado. ii.Si el nuevo estado es un estado objetivo, salir y retornar este estado. iii.Sino, añada el nuevo estado al final de NODE_LIST. b.Para cada forma en que cada regla puede ajustarse al estado descrito en E, haga lo siguiente: 2.Hasta que se encuentre el objetivo o hasta que NODE_LIST esté vacía haga lo siguiente: Algoritmo Primero en Profundidad (DEPTH-FIRST) 1.Si el estado inicial es el objetivo, salir y retornar éxito. a.Genere un sucesor E del estado inicial. Si no hay más sucesores, retorne con señal de fracaso. b.Llame recursivamente al algoritmo, esta vez con E como el estado inicial. c.Si la señal es éxito, retorne, de otra manera, continúe en este lazo. Búsqueda Heurística Para resolver muchos problemas difíciles (explosión combinatoria), es necesario muchas veces llegar a un compromiso de los requerimientos de movilidad y sistematicidad y construir una estructura de control que no necesariamente garantiza el encontrar la mejor respuesta, sino que casi siempre encuentra una buena respuesta. Una técnica heurística mejora la eficiencia del proceso de búsqueda sacrificando, usualmente, exhaustividad. Las consideraciones que sirven de soporte a un proceso de búsqueda heurística, son: Rara vez se requiere, en realidad, una solución óptima. Una buena aproximación, normalmente, sirve muy bien.  A pesar que una aproximación heurística no puede resultar muy buena en el peor de los casos, raras veces aparecen los peores casos en la práctica. El tratar de comprender por qué un heurístico funciona o por qué no funciona, a menudo conduce a una mejor comprensión del problema.    3.6 Busquedas de profundidad En inglés, depth-first search. Si el conjunto open se maneja como una lista LIFO, es decir, como un stack, siempre se estará visitando primero los últimos estados en ser generados. Esto significa que si A genera B y C, y B genera D, antes de visitar C se visita D, que está más alejado de la raiz A, o sea más profundo en el árbol de búsqueda. El algoritmo tiene en este caso la tendencia de profundizar la búsqueda en una rama antes de explorar ramas alternativas.